Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту.
По
определению cos(/CDE)=ED/CD
3/5=ED/14
ED=3*14/5=8,4
По
теореме Пифагора:
CD2=ED2+EC2
142=8,42+EC2
196=70,56+EC2
EC2=125,44
EC=11,2 - это и есть высота
Sтрапеции=EC*(BC+AD)/2
Sтрапеции=11,2*(5+40)/2
Sтрапеции=5,6*45=252
Ответ: Sтрапеции=252
Поделитесь решением
Присоединяйтесь к нам...
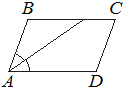Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
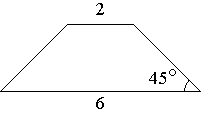В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
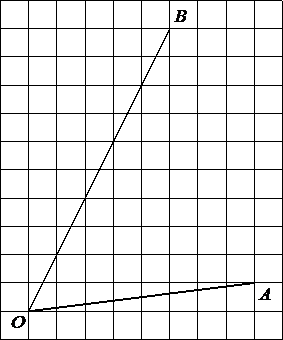Найдите тангенс угла
AOB.
Найдите площадь трапеции, изображённой на рисунке.
Радиус вписанной в квадрат окружности равен 14√
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: