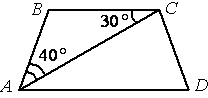Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
AD||BC (по
определению трапеции). Тогда AC является секущей для этих параллельных отрезков.
/BCA=/CAD, т.к. они
внутренние накрест-лежащие.
Тогда /BAD=30°+40°=70°.
По
свойству
равнобедренной трапеции /BAD=/ADC=70°.
Ответ: /ADC=70°.
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Площадь прямоугольного треугольника равна 392√
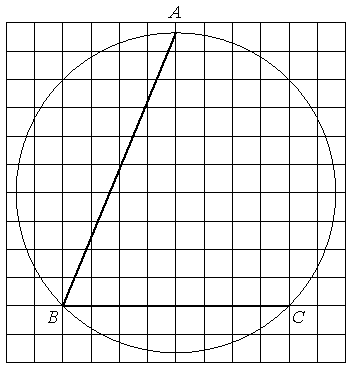Найдите угол ABC. Ответ дайте в градусах.
Синус острого угла A треугольника ABC равен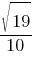 
. Найдите CosA.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: