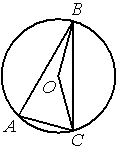
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
По условию ∠BOC=160°, этот угол является
центральным, соответственно дуга ВC (малая часть) тоже равна 160°.
∠BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, ∠BAC=160°/2=80°.
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
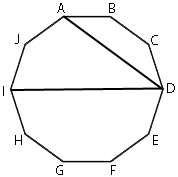ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
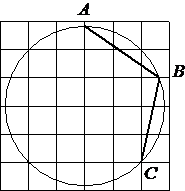Найдите угол ABC . Ответ дайте в градусах.
Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: