ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
Вариант 1 (Предложил пользователь Светлана)
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠DOE) равен 360°/9=40°
Тогда ∠BOG, который опирается на дугу BCDEFG равен:
∠BOG=40°*5=200°
∠BOG является
центральным, следовательно градусная мера дуги BCDEFG тоже равна 200°
∠BAG тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠BAG=200°/2=100° (по
теореме о вписанном угле)
Ответ: 100
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
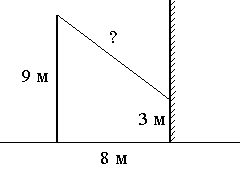От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=19.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-10-18 17:24:17) Валентина: Иногда знания отягощают,т.е.уводят от простого решения.
(2015-01-30 10:48:28) Администратор: Светлана, гениально! Обязательно добавлю Ваше решение...
(2015-01-30 10:25:17) Светлана: Такие задачи проще решать через дугу и вписанный угол. Вписанный угол равен половине дуги на которую опирается. Любой правильный многоугольник можно вписать в окружность. Вершины девятиугольника разделят окружность на 9 дуг, каждая из которых будет равна 40 градусам. Данный угол будет опираться на дугу в 200 градусов. 200:2=100.