
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
Вариант №1 Предложила пользователь Надя.
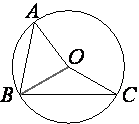 Проведем отрезок OB.
Проведем отрезок OB.
Рассмотрим треугольник AOB.
Так как AO=BO (это радиусы окружности), то данный треугольник
равнобедренный.
Следовательно, ∠OAB=∠ABO=8° (по
свойству равнобедренного треугольника)
∠OBC=∠ABC-∠ABO=15°-8°=7°.
Треугольник BOC тоже
равнобедренный, т.к. OB=OC (радиусы окружности).
Следовательно, ∠OBC=∠BCO=7° (по
свойству).
Ответ: 7.
Вариант №2
 Продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).
Продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).
Рассмотрим треугольник ABE. По
теореме о сумме углов треугольника запишем:
180°=∠OAB+∠ABC+∠BEA
180°=8°+15°+∠BEA
∠BEA=180°-8°-15°=157°
Смежный этому углу ∠OEC=180°-∠BEA=180°-157°=23° (запомним это)
Угол ABC является
вписанным углом, следовательно градусная мера дуги, на которую он опирается, вдвое больше (по
теореме о вписанном угле), т.е. градусная мера дуги AC равна 15°*2=30°
Угол АОС является
центральным и, соответственно, равен градусной мере дуги, на которую опирается. А опирается он на дугу AC, следовательно ∠AOC=30°
Смежный этому углу ∠COE=180°-∠AOC=180°-30°=150°
Рассмотрим треугольник OCE.
По
теореме о сумме углов треугольника запишем:
180°=∠OEC+∠COE+∠OCE
Вспомнив то, что запомнили ранее...
180°=23°+150°+∠OCE
∠OCE=180°-23°-150°=7°
∠OCE и есть искомый угол BCO.
Ответ: ∠BCO=7°
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
 В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
 На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
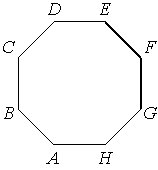 ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
 Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Комментарии:
(2015-05-24 16:29:10) алексей: Большое спасибо разработчикам сайта. Очень помогли.
(2014-11-29 23:16:26) Администратор: Денис, очень неплохое решение. Решений может быть очень много, например доказательств теоремы Пифагора около 600 (если не ошибаюсь).
(2014-11-29 20:55:25) Денис: Я по другому решил. Вот решение, ТОЛЬКО смысл постараюсь передать: 1)в четырехугольнике сумма углов = 360 2)т.к. АВС вписанный угол а АОС центральный опираются на одну и ту жу дугу значит АОС(меньший) =30 градусам. 3) значит угол АОС больший будут равен (360-30)=330 градусам 4)360=(330+8+15+ВСО) 360=345+8+ВСО 15=8+ВСО ВСО=7 градусов Ответ: 7