
 Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Вариант №1
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=∠A+66°+84°
∠A=180°-66°-84°=30°
По
теореме синусов:
2R=BC/sin∠A
2R=BC/sin30°=BC/(1/2)=2BC
R=BC=15
Ответ: 15
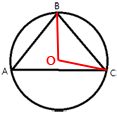 Проведем два отрезка из центра к точкам B и C, как показано на рисунке.
Проведем два отрезка из центра к точкам B и C, как показано на рисунке.Поделитесь решением
Присоединяйтесь к нам...
 Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
 В треугольнике ABC угол C равен 90°, sinA=4/5, AC=9. Найдите AB.
В треугольнике ABC угол C равен 90°, sinA=4/5, AC=9. Найдите AB.
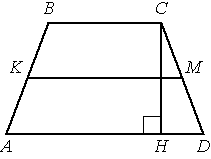 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
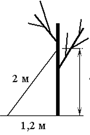 Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
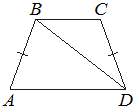 В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
Комментарии: