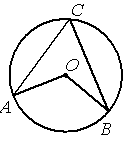
Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=62°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 62°*2=124°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=124°.
Ответ: /AOB=124°.
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD известно, что AD=4, BC=2, а её площадь равна 69. Найдите площадь треугольника ABC.
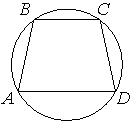Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
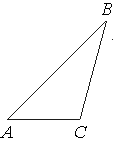В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=44, MN=24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MBN.
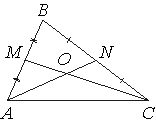Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=18, CM=21. Найдите OM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: