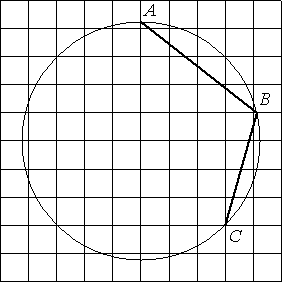
Найдите угол ABC. Ответ дайте в градусах.
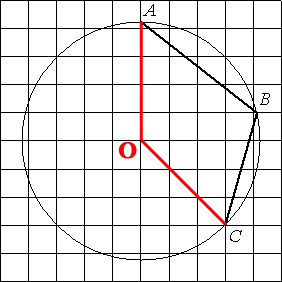Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC равен 135° (прямой угол + половина от прямого угла, 90°+45°=135°).
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается (ABC), тоже равна 135°.
Следовательно, бОльшая дуга имеет градусную меру 360°-135°=225°
∠ABC -
вписанный угол, опирается на бОльшую дугу и по
теореме равен 225°/2=112,5°
Ответ: 112,5
Поделитесь решением
Присоединяйтесь к нам...
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
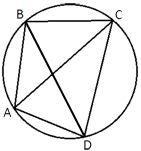Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Площадь прямоугольного треугольника равна
338√
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
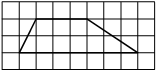На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: