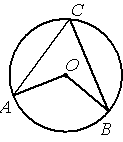
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=128°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 128°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 128/2=64.
Ответ: /ACB=64°.
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
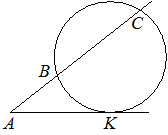Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите этот диаметр, если диаметр описанной окружности треугольника ABC равен 8.
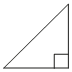В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: