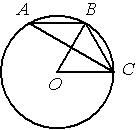
Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=60°, этот угол является
центральным, соответственно дуга ВC тоже равна 60°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 60/2=30.
Ответ: /BAC=30°.
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 2√
Найдите площадь треугольника, изображённого на рисунке.
Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: