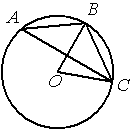
Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
По условию /BOC=70°, этот угол является
центральным, соответственно дуга ВC тоже равна 70°. /BAC - является
вписанным углом и равен половине дуги, на которую опирается (по теореме о вписанном угле). Соответственно, 70/2=35.
Ответ: /BAC=35°.
Поделитесь решением
Присоединяйтесь к нам...
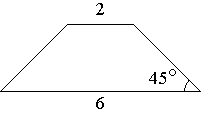В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл) | Прочее оборудование и монтаж | Средн. расход газа/ средн. потребл. мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 24 000 руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 000 руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт*ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости устройства газового и электрического отопления?
Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: