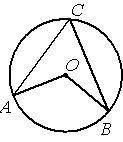
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=70°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 70°*2=140°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=140°.
Ответ: /AOB=140°.
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
Катеты прямоугольного треугольника равны √
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: