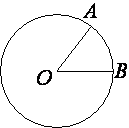
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
∠AOB является центральным, поэтому градусная мера дуги, на которую он опирается тоже равна 66°.
Так как градусная мера всей окружности составляет 360°, то градусная мера большей дуги равна:
360°-66°=294°
Теперь систавим пропорцию:
Для 66° - длина дуги 99
Для 294° - длина дуги x
66/294=99/x
x=294*99/66=294*1,5=441
Ответ: 441
Поделитесь решением
Присоединяйтесь к нам...
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
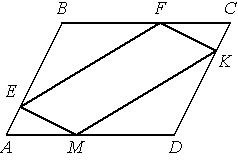В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
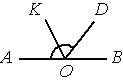Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: