
 В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
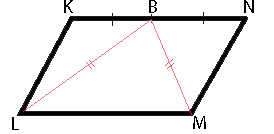
В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники BKL и BNM. KB=BN, т.к. точка B - середина KN, BL=BM (из условия задачи), KL=NM (по свойству параллелограмма). Соответственно, треугольники BKL и BNM равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /BKL=/BNM.
KL||NM (по определению параллелограмма), рассмотрим сторону KN как секущую к этим параллельным сторонам. Тогда получается, что сумма углов BKL и BNM равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны KN и LM, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону KL как секущую к этим параллельным сторонам.
/NKL и /KLM - внутренние односторонние. Следовательно их сумма равна 180°. А так как /NKL=90°, то /KLM тоже равен 90°.
Аналогично доказывается, что /LMN тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
 Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
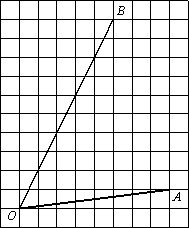 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
 Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.

Комментарии: