В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
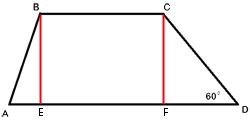Проведем
высоты BE и CF как показано на рисунке.
Рассмотрим треугольник CDF. Он
прямоугольный, т.к. CF-высота.
По
теореме о сумме углов треугольника ∠FCD=180°-90°-60°=30°.
По
определению синуса sin∠FCD=DF/CD=sin30°=1/2
Т.е. DF=CD/2, CD, в свою очередь, по условию задачи равно AD/2, получам, что DF=AD/4.
BC=AD/2 (по условию задачи)
EF=BC=AD/2 (т.к. BCFE - прямоугольник)
Вычислим AE, AE=AD-DF-EF=AD-AD/4-AD/2=AD/4, т.е. мы получили, что AE=FD
Рассмотрим треугольники ABC и DCF:
BE=CF (т.к. BCFE - прямоугольник)
AE=FD (только что получили)
∠AEF=90°=∠DFC, тогда по
первому признаку равенства, треугольники ABC и DCF равны.
Следовательно, AB=CD, т.е. наша
трапеция равнобедренная.
AB=CD=4 (по условию задачи), AD=2*CD=2*BC=8 (тоже по условию), BC=CD=4
FD=AD/4=2
По
теореме Пифагора CD2=CF2+FD2
42=CF2+22
CF2=12, CF=√
CF=2√
SABCD=((BC+AD)/2)*CF=((4+8)/2)*2√
SABCD=12√
Ответ: 12√
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
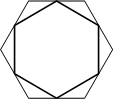Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: