Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
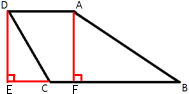Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-150°=30° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin30°=ED/CD (sin30°=1/2 по
таблице)
1/2=ED/33
ED=33*1/2=16,5
sin(∠ABF)=AF/AB (по
определению)
sin60°=ED/AB
AB=ED/sin60° (sin60°=√3/2 по
таблице)
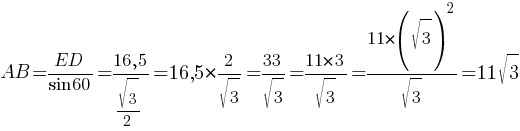
Ответ: 11√3
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведённую к гипотенузе.
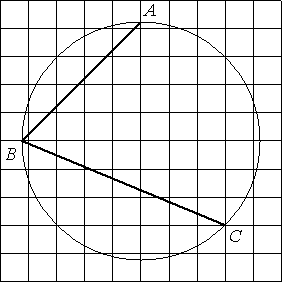Найдите угол ABC. Ответ дайте в градусах.
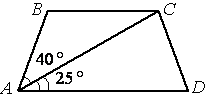Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: