В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Вариант №1 Предложил пользователь Гоша.
Очевидно, что угол OAB это угол DAB, а ∠DAB является вписанным и опирается на дугу BD.
∠OCD тоже является вписанным и опирается на дугу BD.
Тогда, по теореме о вписанном угле, эти углы равны:
∠OCD=∠OAB=70°.
Ответ: 70
Вариант №2
Рассмотрим треугольник АОВ. Этот треугольник
равнобедренный, т.к. ОА и ОВ - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника ∠OAB=∠OBA.
Рассмотрим треугольники АОВ и COD. ∠DOC=∠AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по первому признаку). Поэтому ∠OBA=∠OAB=∠ODC=∠OCD=70°
Ответ: 70
Поделитесь решением
Присоединяйтесь к нам...
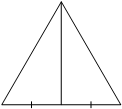Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Синус острого угла A треугольника ABC равен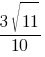 
. Найдите CosA.
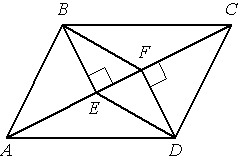В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
Стороны AC, AB, BC треугольника ABC равны 2√
Периметр треугольника равен 54, одна из сторон равна 15,
а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-06-03 21:42:10) Администратор: Гоша, да, действительно. Элегантно и просто. Обязательно скоро размещу такое решение под Вашим именем. Спасибо!
(2019-06-03 12:10:28) гоша: А разве нельзя сразу заключить, что этот угол равен 70 градусам, так как опирается на ту же дугу что и данный угол