
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ347 –Η–Ζ 1087 |
 –ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Β
AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η BC –≤ ―²–Ψ―΅–Κ–Α―Ö K –Η M ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β AC, –Β―¹–Μ–Η BK:KA=3:4, KM=18.
–ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Β
AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η BC –≤ ―²–Ψ―΅–Κ–Α―Ö K –Η M ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –ù–Α–Ι–¥–Η―²–Β AC, –Β―¹–Μ–Η BK:KA=3:4, KM=18.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABC –Η KBM.
/B - –Ψ–±―â–Η–Ι.
/BAC=/BKM (―².–Κ. ―ç―²–Ψ
―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ―΄–Β ―É–≥–Μ―΄)
/BCA=/BMK (―².–Κ. ―ç―²–Ψ ―²–Ψ–Ε–Β
―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ―΄–Β ―É–≥–Μ―΄)
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―ç―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η
–Ω–Ψ–¥–Ψ–±–Ϋ―΄ –Ω–Ψ
–Ω–Β―Ä–≤–Ψ–Φ―É –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É –Ω–Ψ–¥–Ψ–±–Η―è.
–Δ–Ψ–≥–¥–Α –Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é –Ω–Ψ–¥–Ψ–±–Ϋ―΄―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤:
BA/BK=AC/KM
(BK+KA)/BK=AC/KM
1+KA/BK=AC/KM
1+4/3=AC/KM
7/3=AC/18
AC=7*18/3=7*6=42
–û―²–≤–Β―²: AC=42
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
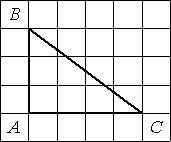 –ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α –Γ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α –Γ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ–Ϋ–Ψ–≥–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
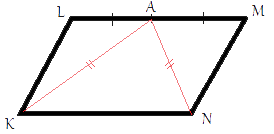 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β KLMN ―²–Ψ―΅–Κ–Α A βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ LM. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ KA=NA. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β KLMN ―²–Ψ―΅–Κ–Α A βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ LM. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ KA=NA. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
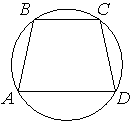 –Θ–≥–Ψ–Μ A ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ–Η AD –Η BC, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, ―Ä–Α–≤–Β–Ϋ 52¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ B ―ç―²–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–Θ–≥–Ψ–Μ A ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ–Η AD –Η BC, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, ―Ä–Α–≤–Β–Ϋ 52¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ B ―ç―²–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –Γ―²–Ψ―Ä–Ψ–Ϋ–Α –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Ϋ–Α 3√2. –ù–Α–Ι–¥–Η―²–Β –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ ―ç―²–Ψ–≥–Ψ –Κ–≤–Α–¥―Ä–Α―²–Α.
–Γ―²–Ψ―Ä–Ψ–Ϋ–Α –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Ϋ–Α 3√2. –ù–Α–Ι–¥–Η―²–Β –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ ―ç―²–Ψ–≥–Ψ –Κ–≤–Α–¥―Ä–Α―²–Α.
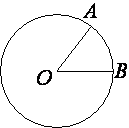 –ù–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A –Η B ―²–Α–Κ, ―΅―²–Ψ ∠AOB=66¬Α. –î–Μ–Η–Ϋ–Α –Φ–Β–Ϋ―¨―à–Β–Ι –¥―É–≥–Η AB ―Ä–Α–≤–Ϋ–Α 99. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –±–Ψ–Μ―¨―à–Β–Ι –¥―É–≥–Η AB.
–ù–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ―²–Φ–Β―΅–Β–Ϋ―΄ ―²–Ψ―΅–Κ–Η A –Η B ―²–Α–Κ, ―΅―²–Ψ ∠AOB=66¬Α. –î–Μ–Η–Ϋ–Α –Φ–Β–Ϋ―¨―à–Β–Ι –¥―É–≥–Η AB ―Ä–Α–≤–Ϋ–Α 99. –ù–Α–Ι–¥–Η―²–Β –¥–Μ–Η–Ϋ―É –±–Ψ–Μ―¨―à–Β–Ι –¥―É–≥–Η AB.

–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: