
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ323 –Є–Ј 1087 |
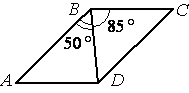 –Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
50¬∞ –Є 85¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
50¬∞ –Є 85¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Я–Њ
—Б–≤–Њ–є—Б—В–≤—Г
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ /B=/D=50¬∞+85¬∞=135¬∞ –Є /A=/C.
–Э–∞–є–і–µ–Љ —Г–≥–ї—Л A –Є C.
–°—В–Њ—А–Њ–љ—Л AD –Є BC –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞). –Х—Б–ї–Є —А–∞—Б—Б–Љ–Њ—В—А–µ—В—М BD –Ї–∞–Ї —Б–µ–Ї—Г—Й—Г—О –Ї —Н—В–Є–Љ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–Љ –њ—А—П–Љ—Л–Љ, —В–Њ —Б—В–∞–љ–Њ–≤–Є—В—Б—П –Њ—З–µ–≤–Є–і–љ—Л–Љ, —З—В–Њ /CBD=/ADB=85¬∞ (—В.–Ї. –Њ–љ–Є
–љ–∞–Ї—А–µ—Б—В –ї–µ–ґ–∞—Й–Є–µ).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABD.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Љ—Л –Љ–Њ–ґ–µ–Љ –љ–∞–њ–Є—Б–∞—В—М: 180¬∞=/ABD+/BDA+/A
180°=50°+85°+/A
/A=45°=/C
135>45, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Г–≥–ї—Л A –Є C - –Љ–µ–љ—М—И–Є–µ.
–Ю—В–≤–µ—В: –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 45¬∞.
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Э–∞ —Б—В–Њ—А–Њ–љ–µ BC –Њ—Б—В—А–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC (AB≠AC) –Ї–∞–Ї –љ–∞ –і–Є–∞–Љ–µ—В—А–µ –њ–Њ—Б—В—А–Њ–µ–љ–∞ –њ–Њ–ї—Г–Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –њ–µ—А–µ—Б–µ–Ї–∞—О—Й–∞—П –≤—Л—Б–Њ—В—Г AD –≤ —В–Њ—З–Ї–µ M, AD=32, MD=8, H вАФ —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤—Л—Б–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC. –Э–∞–є–і–Є—В–µ AH.
–Э–∞ —Б—В–Њ—А–Њ–љ–µ BC –Њ—Б—В—А–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC (AB≠AC) –Ї–∞–Ї –љ–∞ –і–Є–∞–Љ–µ—В—А–µ –њ–Њ—Б—В—А–Њ–µ–љ–∞ –њ–Њ–ї—Г–Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, –њ–µ—А–µ—Б–µ–Ї–∞—О—Й–∞—П –≤—Л—Б–Њ—В—Г AD –≤ —В–Њ—З–Ї–µ M, AD=32, MD=8, H вАФ —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤—Л—Б–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC. –Э–∞–є–і–Є—В–µ AH.
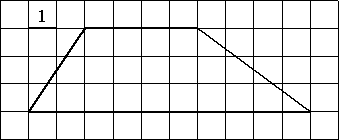 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
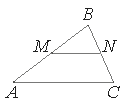 –Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, AC=36, MN=28. –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–∞ 162. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ MBN.
–Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, AC=36, MN=28. –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–∞ 162. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ MBN.
–Ъ–∞–Ї–Є–µ –Є–Ј –і–∞–љ–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ—Л? –Ч–∞–њ–Є—И–Є—В–µ –Є—Е –љ–Њ–Љ–µ—А–∞.
1) –Я—А–Њ—В–Є–≤ –±–Њ–ї—М—И–µ–є —Б—В–Њ—А–Њ–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –ї–µ–ґ–Є—В –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї.
2) –Ы—О–±–Њ–є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М.
3) –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Љ–µ–љ—М—И–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –і–≤—Г—Е –µ–≥–Њ —Б—В–Њ—А–Њ–љ.
 –°—В–Њ—А–Њ–љ–∞ AB –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AD. –Ґ–Њ—З–Ї–∞ K вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AB. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ DK вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC.
–°—В–Њ—А–Њ–љ–∞ AB –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AD. –Ґ–Њ—З–Ї–∞ K вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AB. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ DK вАФ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: