
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ156 –Η–Ζ 1087 |
 –ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ –Κ–Ψ–Μ–Ψ–¥–Β―Ü ―¹ ¬Ϊ–Ε―É―Ä–Α–≤–Μ―ë–Φ¬Μ. –ö–Ψ―Ä–Ψ―²–Κ–Ψ–Β –Ω–Μ–Β―΅–Ψ –Η–Φ–Β–Β―² –¥–Μ–Η–Ϋ―É 2 –Φ, –Α –¥–Μ–Η–Ϋ–Ϋ–Ψ–Β –Ω–Μ–Β―΅–Ψ βÄî 4 –Φ. –ù–Α ―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Φ–Β―²―Ä–Ψ–≤ –Ψ–Ω―É―¹―²–Η―²―¹―è –Κ–Ψ–Ϋ–Β―Ü –¥–Μ–Η–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α, –Κ–Ψ–≥–¥–Α –Κ–Ψ–Ϋ–Β―Ü –Κ–Ψ―Ä–Ψ―²–Κ–Ψ–≥–Ψ –Ω–Ψ–¥–Ϋ–Η–Φ–Β―²―¹―è –Ϋ–Α 1,5 –Φ?
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Β –Η–Ζ–Ψ–±―Ä–Α–Ε―ë–Ϋ –Κ–Ψ–Μ–Ψ–¥–Β―Ü ―¹ ¬Ϊ–Ε―É―Ä–Α–≤–Μ―ë–Φ¬Μ. –ö–Ψ―Ä–Ψ―²–Κ–Ψ–Β –Ω–Μ–Β―΅–Ψ –Η–Φ–Β–Β―² –¥–Μ–Η–Ϋ―É 2 –Φ, –Α –¥–Μ–Η–Ϋ–Ϋ–Ψ–Β –Ω–Μ–Β―΅–Ψ βÄî 4 –Φ. –ù–Α ―¹–Κ–Ψ–Μ―¨–Κ–Ψ –Φ–Β―²―Ä–Ψ–≤ –Ψ–Ω―É―¹―²–Η―²―¹―è –Κ–Ψ–Ϋ–Β―Ü –¥–Μ–Η–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α, –Κ–Ψ–≥–¥–Α –Κ–Ψ–Ϋ–Β―Ü –Κ–Ψ―Ä–Ψ―²–Κ–Ψ–≥–Ψ –Ω–Ψ–¥–Ϋ–Η–Φ–Β―²―¹―è –Ϋ–Α 1,5 –Φ?
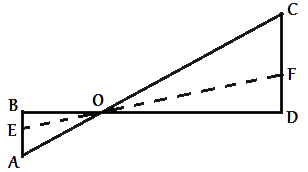 –†–Η―¹―É–Ϋ–Ψ–Κ,–Ω―Ä–Β–¥–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –≤ –Ζ–Α–¥–Α―΅–Β –Φ–Ψ–Ε–Ϋ–Ψ ―É―¹–Μ–Ψ–≤–Ϋ–Ψ –Ω–Β―Ä–Β―Ä–Η―¹–Ψ–≤–Α―²―¨ –≤ –≤–Η–¥–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤. –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABO –Η COD.
–†–Η―¹―É–Ϋ–Ψ–Κ,–Ω―Ä–Β–¥–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –≤ –Ζ–Α–¥–Α―΅–Β –Φ–Ψ–Ε–Ϋ–Ψ ―É―¹–Μ–Ψ–≤–Ϋ–Ψ –Ω–Β―Ä–Β―Ä–Η―¹–Ψ–≤–Α―²―¨ –≤ –≤–Η–¥–Β ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤. –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABO –Η COD.
1) /BOA=/DOC, ―².–Κ. –Ψ–Ϋ–Η
–≤–Β―Ä―²–Η–Κ–Α–Μ―¨–Ϋ―΄–Β.
2) /OBA=/ODC=90¬Α
3) /BAO=/DCO, ―².–Κ. –Ψ–Ϋ–Η
–≤–Ϋ―É―²―Ä–Β–Ϋ–Ϋ–Η–Β –Ϋ–Α–Κ―Ä–Β―¹―²-–Μ–Β–Ε–Α―â–Η–Β.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABO –Η COD
–Ω–Ψ–¥–Ψ–±–Ϋ―΄ (–Ω–Ψ –Ω―Ä–Η–Ζ–Ϋ–Α–Κ―É –Ω–Ψ–¥–Ψ–±–Η―è). –û―²―¹―é–¥–Α ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ CO/AO=CD/AB. –ü–Ψ―ç―²–Ψ–Φ―É –Ω―Ä–Η –¥–≤–Η–Ε–Β–Ϋ–Η–Η, –≤―΄―¹–Ψ―²–Α –Κ–Ψ–Ϋ―Ü–Ψ–≤ –Ε―É―Ä–Α–≤–Μ―è –±―É–¥–Β―² –Ω–Ψ–¥―΅–Η–Ϋ―è―²―¨―¹―è ―ç―²–Ψ–Ι –Ε–Β –Ω―Ä–Ψ–Ω–Ψ―Ä―Ü–Η–Η.
CO/AO=CD/AB=CF/AE
4/2=CF/1,5 => CF=4*1,5/2=3.
–û―²–≤–Β―²: –Κ–Ψ–Ϋ–Β―Ü –¥–Μ–Η–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Μ–Β―΅–Α –Ψ–Ω―É―¹―²–Η―²―¹―è –Ϋ–Α 3 –Φ–Β―²―Ä–Α.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –Γ―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 12√3. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–Γ―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 12√3. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
 –£―΄―¹–Ψ―²–Α AH ―Ä–Ψ–Φ–±–Α ABCD –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É CD –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η DH=8 –Η CH=2. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É ―Ä–Ψ–Φ–±–Α.
–£―΄―¹–Ψ―²–Α AH ―Ä–Ψ–Φ–±–Α ABCD –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É CD –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η DH=8 –Η CH=2. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É ―Ä–Ψ–Φ–±–Α.
 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Κ–≤–Α–¥―Ä–Α―²–Α, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Ψ–Κ–Ψ–Μ–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–¥–Η―É―¹–Α 32.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Κ–≤–Α–¥―Ä–Α―²–Α, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Ψ–Κ–Ψ–Μ–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–¥–Η―É―¹–Α 32.
 –ü–Β―Ä–Η–Φ–Β―²―Ä ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Β–Ϋ 48, –Ψ–¥–Ϋ–Α –Η–Ζ ―¹―²–Ψ―Ä–Ψ–Ϋ ―Ä–Α–≤–Ϋ–Α 18,
–Α ―Ä–Α–¥–Η―É―¹ –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ –Ϋ–Β–≥–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 3. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–ü–Β―Ä–Η–Φ–Β―²―Ä ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Β–Ϋ 48, –Ψ–¥–Ϋ–Α –Η–Ζ ―¹―²–Ψ―Ä–Ψ–Ϋ ―Ä–Α–≤–Ϋ–Α 18,
–Α ―Ä–Α–¥–Η―É―¹ –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ –Ϋ–Β–≥–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 3. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
 –ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 25, –Α –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β ―Ä–Α–≤–Ϋ–Ψ 48. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–ë–Ψ–Κ–Ψ–≤–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 25, –Α –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β ―Ä–Α–≤–Ϋ–Ψ 48. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.

–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: