Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
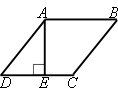150° - это тупой угол, т.е. это ∠DAB и ∠BCD (эти углы равны по
свойству параллелограмма и ромба).
AB||CD (по определению параллелограмма и ромба).
Тогда:
∠DEA=∠BAE=90° (это
накрест лежащие углы).
Следовательно:
∠DAE=∠DAB-∠EAB=150°-90°=60°
Треугольник DAE - прямоугольный, тогда, по определению косинуса:
cos∠EAB=AE/AD
cos60°=AE/38
1/2=AE/38 (по таблице косинусов)
AE=38/2=19 - это и есть
высота.
Ответ: 19
Поделитесь решением
Присоединяйтесь к нам...
Сколько досок длиной 4 м, шириной 20 см и толщиной 30 мм выйдет из бруса длиной 80 дм, имеющего в сечении прямоугольник размером 30 см на 40 см?
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
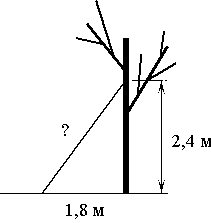Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-12-19 12:31:20) Fdggf: Fezzxc!???