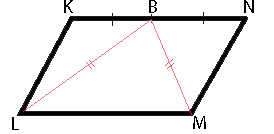
В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники BKL и BNM. KB=BN, т.к. точка B - середина KN, BL=BM (из условия задачи), KL=NM (по свойству параллелограмма). Соответственно, треугольники BKL и BNM равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /BKL=/BNM.
KL||NM (по определению параллелограмма), рассмотрим сторону KN как секущую к этим параллельным сторонам. Тогда получается, что сумма углов BKL и BNM равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны KN и LM, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону KL как секущую к этим параллельным сторонам.
/NKL и /KLM - внутренние односторонние. Следовательно их сумма равна 180°. А так как /NKL=90°, то /KLM тоже равен 90°.
Аналогично доказывается, что /LMN тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
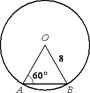Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.
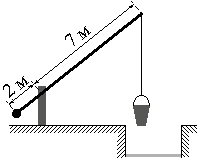На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Стороны AC, AB, BC треугольника ABC равны 3√
Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: