На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
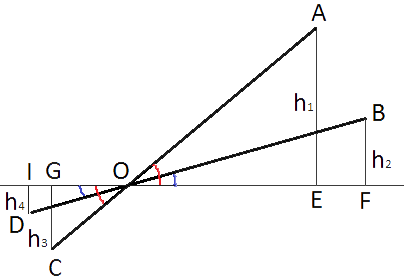Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников.
h1 - изначальная высота длинного плеча журавля.
h2 - конечная высота длинного плеча журавля.
h3 - изначальная высота короткого плеча журавля.
h4 - конечная высота короткого плеча журавля.
h3-h4=0,5 метра (по условию задачи).
Нам надо найти:
h1-h2=?.
Рассмотрим треугольники AOE и COG.
1) ∠AOE=∠COG, т.к. они
вертикальные.
2) ∠AEO=∠CGO=90°
Следовательно, треугольники AOE и COG
подобны (по первому признаку подобия). Отсюда следует, что h1/OA=h3/OC.
Треугольники BOF и DOI тоже
подобны (аналогично предыдущим треугольникам).
Тогда:
h2/OB=h4/OD
OA=OB и OC=OD (так как длины плеч журавля не меняются), тогда:
h2/OA=h4/OC
Вычтем из первого равенства второе:
h1/OA-h2/OA=h3/OC-h4/OC.
(h1-h2)/OA=(h3-h4)/OC.
(h1-h2)/6=0,5/2.
h1-h2=6*0,5/2=1,5.
Ответ: 1,5.
Поделитесь решением
Присоединяйтесь к нам...
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 11°?
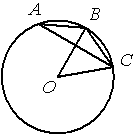Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-21 21:34:00) Елена: Опускаем перпендикуляры из С на ВD и из А на ВD. Полученные треугольники подобны, т.к. проведённые перпендикуляры параллельны друг другу. Дальше составляем пропорцию и находим неизвестный перпендикуляр.
(2015-03-14 13:23:46) Николай: А ещё можно на глаз определить, по клеточкам))