Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
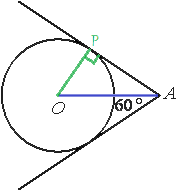Проведем отрезок АО. Обозначим одну из точек касания окружности и касательной как Р. Проведем отрезок ОР. ОР является радиусом и перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР. Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР. АО является биссектрисой угла, образованного касательными (свойство касательных прямых). Соответственно угол РАО равен половине данного угла, т.е. 30°. Синус угла PAO равен 1/2 (табличное значение) и равен отношению ОР к АО (по определению синуса). Соответственно, ОР равняется половине АО. AO=2*ОР=2*6=12.
Ответ: AO=12.
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Найдите площадь параллелограмма, изображённого на рисунке.
В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
Синус острого угла A треугольника ABC равен 
. Найдите CosA.
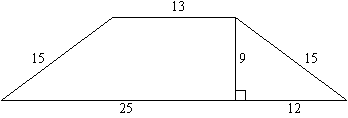Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: