
При каких значениях m вершины парабол у=х2+4mх+2m и у=-х2+2mх+4 расположены по одну сторону от оси х?
Иными словами можно сказать так: при каких m координата y вершин парабол будет или положительной, или отрицательной для обоих парабол одновременно.
Определим координаты y вершин парабол по
формуле:
Для первой параболы:
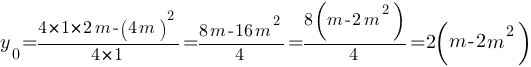
Для второй параболы:
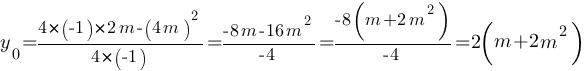
Теперь рассмотрим первый вариант: вершины обеих парабол лежат выше оси Х, т.е. больше нуля.
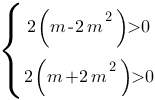
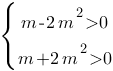
Решив систему неравенств мы найдем все такие m, при которых вершины обеих парабол лежат выше оси Х.
Чтобы решить систему неравенств, необходимо решить отдельно каждое неравенство и пересечь полученные диапазоны. Пересечение диапазонов и будет решением системы неравенств.
1) m-2m2>0
Для решения неравенства найдем корни соответствующего квадратного уравнения:
m-2m2=0
m(1-2m)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому:
m1=0
m2=0,5
Ветви параболы m-2m2 направлены вниз, так как коэффициент а=-2, т.е. меньше нуля.
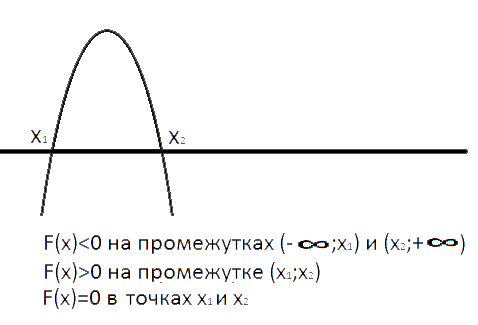 m-2m2>0 на диапазоне (0; 0,5).
m-2m2>0 на диапазоне (0; 0,5).
2) m+2m2>0
Тем же способом находим корни:
m1=0
m2=-0,5
Ветви параболы m+2m2 направлены вверх, так как коэффициент а=2, т.е. больше нуля.
 m+2m2>0 на диапазонах (-∞; -0,5)∪(0; +∞).
m+2m2>0 на диапазонах (-∞; -0,5)∪(0; +∞).
Пересекая диапазоны, мы получаем решение системы неравенств:
m⊂(0; 0,5) - при таких значениях m вершины обеих парабол будут выше оси Х.
Теперь рассмотрим вариант, когда обе параболы находятся ниже оси Х.
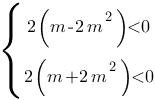
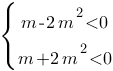
Решаем эту систему тем же способом:
1) m-2m2<0
m(1-2m)<0
Корни:
m1=0
m2=0,5
 (-∞; 0)∪(0,5; +∞).
(-∞; 0)∪(0,5; +∞).
2) m+2m2<0
m(1+2m)<0
Корни:
m1=0
m2=-0,5
 (-0,5; 0).
(-0,5; 0).
Пересекая диапазоны, получаем (-0,5; 0).
Итоговый ответ будет сложением двух полученных диапазонов: (0; 0,5) и (-0,5; 0).
Ответ: (-0,5; 0)∪(0; 0,5)
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения (x-5)2-x(10+x) при x=-1/20.
Постройте график функции 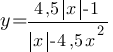 и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
Решите систему уравнений 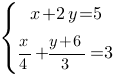
Найдите значение выражения (1,8*10-3)(7*10-2).
Магазин закупил на складе футболки и стал продавать их по цене на 70% больше закупочной. В конце года цена была снижена на 40%. Какая цена больше: та, по которой магазин закупил футболки, или их цена в конце года – и на сколько процентов?
Комментарии: