Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
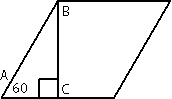Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). ∠A=60°, следовательно по
теореме о сумме углов треугольника ∠АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=26/2=13. Следовательно вторая половина стороны ромба = 26-13=13. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
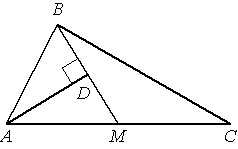Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
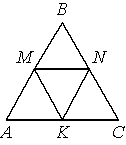В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-11-03 00:08:26) Администратор: Елена, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-10-23 22:02:17) елена: . Площадь ромба равна 18, а периметр равен 36. Найдите высоту ромба.