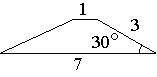
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 1 и 7.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
Проведем высоту как показано на рисунке. Получившийся треугольник является
прямоугольным. По
определению синуса можем записать: sin30°=h/3 => h=3*sin30°, sin30°=1/2 (
табличное значение).
h=3*1/2=1,5.
Sтрапеции=(1+7)/2*1,5=6
Ответ: площадь трапеции равна 6.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 163°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
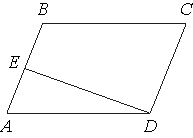Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: