Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
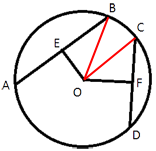Проведем отрезки OB и OC, как показано на рисунке.
Расстоянием от точки до прямой является длина перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои
хорды пополам (по
свойству хорды)
Получается, что треугольники OEB и OCF -
прямоугольные, EB=AB/2 и CF=CD/2.
По
теореме Пифагора:
OB2=OE2+EB2
OB2=242+(20/2)2
OB2=576+100=676
OB=√676=26
OB=OC=26 (т.к. OB и OC - радиусы окружности)
По
теореме Пифагора:
OC2=CF2+FO2
OC2=(CD/2)2+FO2
262=(48/2)2+FO2
676=576+FO2
FO2=676-576=100
FO=√100=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
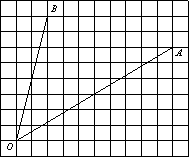Найдите тангенс угла AOB.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: