Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA=∠BAE (т.к. AE -
биссектриса).
Получается, что треугольник ABE -
равнобедренный.
BF -
биссектриса, а по
свойству равнобедренного треугольника, она так же и
медиана и
высота.
Таким образом, получается, что треугольник ABF -
прямоугольный.
По
теореме Пифагора:
AB2=AF2+BF2
AB2=212+202
AB2=441+400=841
AB=√841=29
Ответ: 29
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
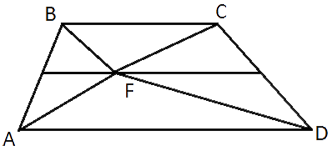На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
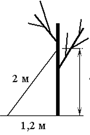Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
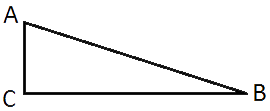Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: