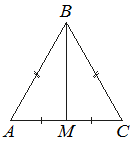В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
По
третьему свойству равнобедренного треугольника, BM является не только медианой, но и
высотой.
Следовательно, треугольник ABM -
прямоугольный.
Тогда tgA=BM/AM (по определению tg).
А так как по условию thA=12/5, то:
BM/AM=12/5
12/AM=12/5 |:12
1/AM=1/5
AM=5
AM и BM - катеты треугольника ABM. Необходимо найти AB. Воспользуемся
теоремой Пифагора:
AB2=AM2+BM2
AB2=52+122
AB2=25+144=169
AB=√169=13
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
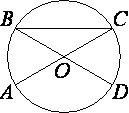В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.
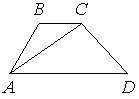В трапеции ABCD известно, что AD=8, BC=7, а её площадь равна 45. Найдите площадь треугольника ABC.
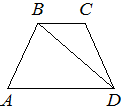В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
На плане указано, что прямоугольная комната имеет площадь 20,1 кв. м. Точные измерения показали, что ширина комнаты равна 4 м,
а длина 5,1 м. На сколько квадратных метров площадь комнаты отличается от площади, указанной на плане?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: