Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=44, MN=24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MBN.
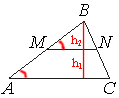Рассмотрим треугольники ABC и MBN.
∠ABC - общий.
∠BAC=∠BMN
Следовательно, по первому признаку подобия, эти треугольники подобны.
Площади треугольника ABC:
SABC=(1/2)AC*h1
121=(1/2)*44*h1
h1=121*2/44=121/22=5,5
Из подобия треугольников получаем пропорцию:
AC/MN=h1/h2
h2=MN*h1/AC=24*5,5/44=24/8=3
Тогда площадь треугольника MBN:
SMBN=(1/2)MN*h2
SMBN=(1/2)*24*3=12*3=36
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Площадь прямоугольного треугольника равна 882√
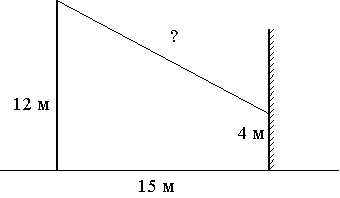От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: