Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Рассмотрим треугольники ABC и MBN.
∠ABC - общий
∠BAC=∠BMN (соответственные углы)
Следовательно, по первому признаку подобия, данные треугольники
подобны (по двум углам).
Поэтому мы можем записать пропорцию соотношения сторон
подобных треугольников:
MN/AC=MB/AB
14/21=MB/24
MB=14*24/21=2*24/3=2*8=16
AM=AB-MB=24-16=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
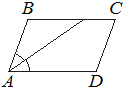Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
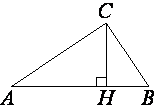В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
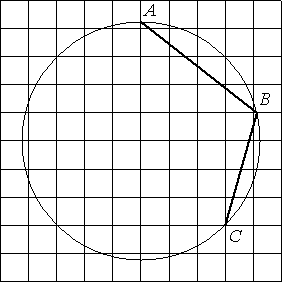Найдите угол ABC. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: