На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
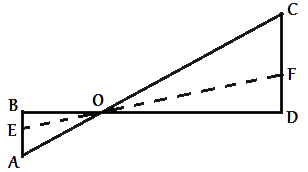Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников. Рассмотрим треугольники ABO и COD.
1) /BOA=/DOC, т.к. они
вертикальные.
2) /OBA=/ODC=90°
3) /BAO=/DCO, т.к. они
внутренние накрест-лежащие.
Следовательно, треугольники ABO и COD
подобны (по признаку подобия). Отсюда следует, что CO/AO=CD/AB. Поэтому при движении, высота концов журавля будет подчиняться этой же пропорции.
CO/AO=CD/AB=CF/AE
4/2=CF/1,5 => CF=4*1,5/2=3.
Ответ: конец длинного плеча опустится на 3 метра.
Поделитесь решением
Присоединяйтесь к нам...
Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
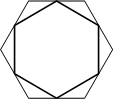Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
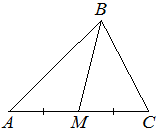В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
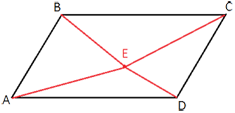Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
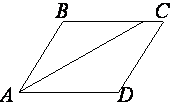Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: