
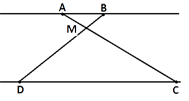 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
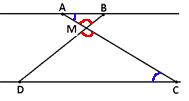 Рассмотрим треугольники ABM и CDM.
Рассмотрим треугольники ABM и CDM.
∠AMB=∠CMD (так как они
вертикальные).
∠BAM=∠MCD (так как они
внутренние накрест-лежащие).
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, мы можем записать:
DC/AB=MC/AM
30/15=MC/AM
2=MC/AM
MC=2AM
AC=AM+MC (по рисунку)
39=AM+2AM
39=3AM
AM=13
MC=2AM=2*13=26
ответ: MC=26
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
3) Площадь круга меньше квадрата длины его диаметра.
 В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
 Площадь равнобедренного треугольника равна 1600√
Площадь равнобедренного треугольника равна 1600√
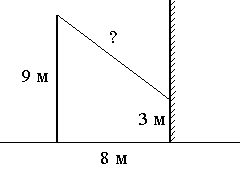 От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Комментарии: