На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?
Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE:
∠C - общий
∠B=∠DEC=90°
Тогда, по первому признаку данные треугольники подобны.
Следовательно, мы можем записать пропорцию:
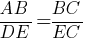
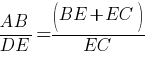
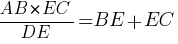
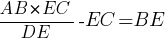
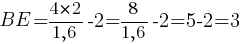
Ответ: 3
Поделитесь решением
Присоединяйтесь к нам...
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
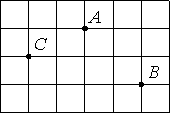На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
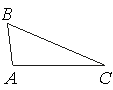В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
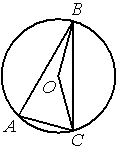Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
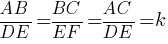
Комментарии:
(2017-11-26 20:46:55) Администратор: Дарья, я доработал немного решение, чтобы стало все понятно и очевидно.
(2017-11-24 16:31:52) Дарья: Как могло получится в ответе 3,если 1,6-2 в результате получится отрицательное число?