Радиус вписанной в квадрат окружности равен 14√
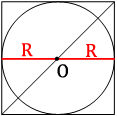Проведем радиусы окружности, как показано на рисунке.
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, т.е.:
a=2R=2*14√
По свойству квадрата, все углы прямые.
Следовательно, треугольник, образованный двумя сторонами и диагональю (обозначим ее как b) - прямоугольный.
Тогда можем применить теорему Пифагора:
b2=a2+a2
b2=2a2
b2=2(28√
b2=2*282*2
b2=282*22=(28*2)2=562
b=56
Ответ: 56
Поделитесь решением
Присоединяйтесь к нам...
Косинус острого угла A треугольника ABC равен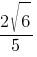 
. Найдите sinA.
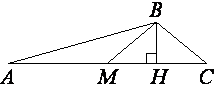В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-02-21 09:52:16) Администратор: Майкл, Вы правы, в решение вкралась ошибка. Спасибо большое, что заметили. Все исправлено!
(2019-02-21 00:54:00) Майкл: У вас получается , что лишь половина диагонали равно 28 , так как вы брали маленький треугольник , а просили Диагональ квадрата .Если а=14 корней из 2 ( то есть радиус , то тогда у вас диагональ меньше , чем сторона квадрата , а это невозможно.28 корней из двух больше 28