
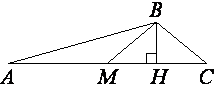 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
Так как BM -
медиана, значит AM=MC=AC/2=64/2=32
Рассмотрим треугольник MBC.
MH=MC-HC=32-16=16, т.е. получается, что MC=HC.
BH для этого треугольника получается не только
высота, но и
медиана. Это
свойство
равнобедренного треугольника.
По
свойству равнобедренного
треугольника: ∠BMC=∠ACB=37°.
∠AMB=180°-∠BMC=180°-37°=143° (т.к. он
смежный)
Ответ: 143
Поделитесь решением
Присоединяйтесь к нам...
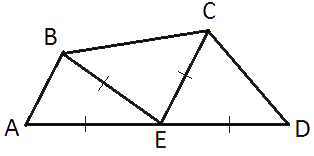 Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
 В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
 В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
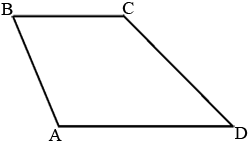 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Комментарии: