В треугольнике ABC угол C равен 90°, sinA=8/9, AC=2√
По
определению sinA=BC/AB=8/9
BC=8AB/9
По
теореме Пифагора:
AB2=BC2+AC2
AB2=(8AB/9)2+AC2
AB2=64AB2/81+(2√
AB2-64AB2/81=4*17
(81AB2-64AB2)/81=68
17AB2=81*68
AB2=81*4=324
AB=18
Ответ: AB=18
Поделитесь решением
Присоединяйтесь к нам...
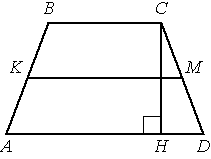В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
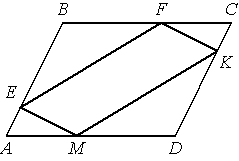В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: