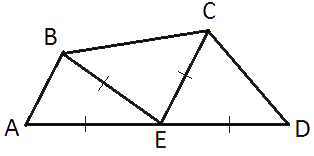
Середина M стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°.
Сумма углов любого выпуклого n-угольника равна (n-2)180, тогда сумма углов четырехугольника (4-2)180=360.
Т.е. ∠A+∠B+∠C+∠D=360
∠A+129°+96°+∠D=360°
∠A+∠D=135°
Треугольники AEB, BEC и ECD -
равнобедренные, т.к. стороны AE=EB=EC=ED.
Следовательно:
∠A=∠ABE
∠EBC=∠ECB
∠ECD=∠D
Использую сумму углов четырехугольника, запишем:
∠A+∠ABE+∠EBC+∠ECB+∠ECD+∠D=360°
Используя ранее полученные равенства, запишем:
∠A+∠A+2∠EBC+∠D+∠D=360°
2∠A+2∠EBC+2∠D=360°
∠A+∠EBC+∠D=180°
135°+∠EBC=180°
∠EBC=45°
Рассмотрим треугольник EBC.
BE=CE (по условию задачи)
Следовательно, треугольник EBC
равнобедренный.
По
свойству равнобедренного треугольника:
∠EBC=∠ECB=45°
По
теореме о сумме углов треугольника:
180°=∠EBC+∠ECB+∠BEC
180°=45°+45°+∠BEC
∠BEC=90°
Получается, что треугольник EBC не только
равнобедренный, но и
прямоугольный.
Тогда по
теореме Пифагора:
BC2=BE2+CE2
64=BE2+CE2
Так как BE=CE, то BE2=CE2=64/2=32
BE=CE=√
AD=AE+ED=√
Ответ: AD=8√
Поделитесь решением
Присоединяйтесь к нам...
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
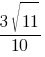В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: