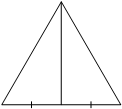
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Введем обозначения как показано на рисунке.
По
определению равностороннего треугольника:
AB=BC=AC=14√3
По
свойству равностороннего треугольника, медиана является так же и
биссектрисой, и
высотой.
Следовательно:
1) BD перпендикулярен AC (т.к. BD -
высота), т.е. треугольник ABD -
прямоугольный.
2) AD=AC/2 (т.к. AC - медиана).
По
теореме Пифагора:
AB2=BD2+AD2
AB2=BD2+(AC/2)2
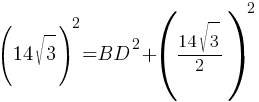
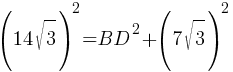
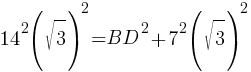
196*3=BD2+49*3
588=BD2+147
BD2=588-147=441
BD=√441=21
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
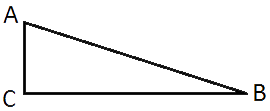Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
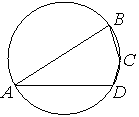Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
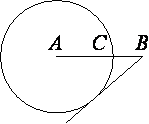На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: