Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
AB=BC=CD=AD=DH+CH=24+2=26 (по
определению ромба).
Рассмотрим треугольник AHD.
AHD -
прямоугольный (т.к. AH -
высота), тогда по
теореме Пифагора:
AD2=AH2+DH2
262=AH2+242
676=AH2+576
AH2=676-576=100
AH=√100=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
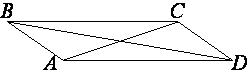В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: