Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
FO=RO (т.к. это радиусы окружности)
FO=RO=FQ=QR (по
определению ромба)
Проведем отрезок OQ.
OQ тоже радиус окружности, следовательно OQ=FO=RO=FQ=QR
Следовательно, треугольники FQO и QRO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно, /ORQ=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
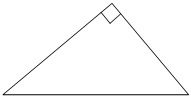Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: