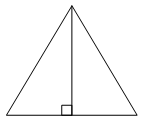
Высота равностороннего треугольника равна 15√
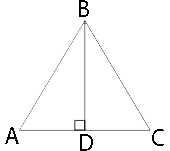Так как треугольник
равносторонний, то все его стороны равны. Обозначим длину стороны как a.
По
второму свойству равностороннего треугольника:
BD=√
15√
15*2*√
Периметр треугольника равен:
P=AB+BC+AD=a+a+a=3a=3*30=90
Ответ: P=90
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=38°. Найдите угол NMB. Ответ дайте в градусах.
Площадь равнобедренного треугольника равна 196√
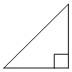В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-15 15:47:45) Сергей: а все по св-ву
(2015-05-15 15:47:06) Сергей: Откуда мы взяли 3а в квадрате деленое на 2
(2015-01-23 23:27:47) Администратор: Конечно "а", а не "х". Исправлено.
(2015-01-23 18:54:18) : Откуда взяли 3X?