
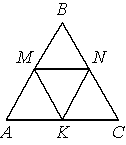
 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
По условию задачи AB=BC=CA (т.к. треугольник ABC -
равносторонний). Значит AK=KC=CN=NB=BM=MA.
Тогда, MK -
средняя линия треугольника ABC. Следовательно, MK=BN и MK||BN (по
теореме о средней линии).
NK - тоже
средняя линия, равна BM и параллельна BM.
Получается, что MK=BN=BM=NK, т.е. BMNK -
ромб (по
свойству ромба).
Поделитесь решением
Присоединяйтесь к нам...
 В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
 В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
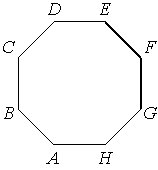 ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
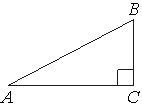 В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Комментарии: