
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ333 –Є–Ј 1087 |
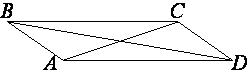 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –і–Є–∞–≥–Њ–љ–∞–ї—М AC –≤ 2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AB –Є ∠ACD=104¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –і–Є–∞–≥–Њ–љ–∞–ї—М AC –≤ 2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AB –Є ∠ACD=104¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
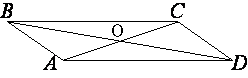 –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —В–Њ—З–Ї—Г –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є –Ї–∞–Ї –Ю.
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ —В–Њ—З–Ї—Г –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є –Ї–∞–Ї –Ю.
–Я–Њ
—Б–≤–Њ–є—Б—В–≤—Г
–њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ AO=OC=AC/2.
AB=CD (–њ–Њ
–і—А—Г–≥–Њ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г).
–Р —В–∞–Ї –Ї–∞–Ї AC –≤ 2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AB (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є), —В–Њ OC=AB=CD.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї OCD -
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
–Я–Њ
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ∠COD=∠CDO.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞: 180¬∞=∠COD+∠CDO+∠ACD=∠COD+∠CDO+104¬∞
∠COD+∠CDO=76¬∞, –∞ —В–∞–Ї –Ї–∞–Ї ∠COD=∠CDO (—Н—В–Њ –Љ—Л –≤—Л—П—Б–љ–Є–ї–Є —А–∞–љ–µ–µ), —В–Њ ∠COD=∠CDO=76¬∞/2=38¬∞
∠COD - –Њ—Б—В—А—Л–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ,
∠COB=180¬∞-∠COD=180¬∞-38¬∞=142¬∞ (—В.–Ї. —Н—В–Њ
—Б–Љ–µ–ґ–љ—Л–µ —Г–≥–ї—Л) - —В—Г–њ–Њ–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є.
–Ю—В–≤–µ—В: –Њ—Б—В—А—Л–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ (∠COD) —А–∞–≤–µ–љ 38¬∞, —В—Г–њ–Њ–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є —А–∞–≤–µ–љ 142¬∞.
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
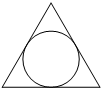 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —А–∞–≤–µ–љ 10√3. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, —А–∞–≤–µ–љ 10√3. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –і–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ O. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –≤ —З–µ—В—Л—А–µ —А–∞–Ј–∞ –±–Њ–ї—М—И–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ COD.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AL, —Г–≥–Њ–ї ALC —А–∞–≤–µ–љ 148¬∞, —Г–≥–Њ–ї ABC —А–∞–≤–µ–љ 132¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AL, —Г–≥–Њ–ї ALC —А–∞–≤–µ–љ 148¬∞, —Г–≥–Њ–ї ABC —А–∞–≤–µ–љ 132¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 2√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 2√
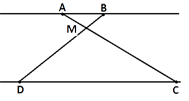 –Ю—В—А–µ–Ј–Ї–Є AB –Є DC –ї–µ–ґ–∞—В –љ–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ—А—П–Љ—Л—Е, –∞ –Њ—В—А–µ–Ј–Ї–Є AC –Є вАЙBD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ M. –Э–∞–є–і–Є—В–µ MC, –µ—Б–ї–Є AB=15, DC=30, AC=39.
–Ю—В—А–µ–Ј–Ї–Є AB –Є DC –ї–µ–ґ–∞—В –љ–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ—А—П–Љ—Л—Е, –∞ –Њ—В—А–µ–Ј–Ї–Є AC –Є вАЙBD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ M. –Э–∞–є–і–Є—В–µ MC, –µ—Б–ї–Є AB=15, DC=30, AC=39.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2020-04-15 11:22:04) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ы–µ—И–∞, –Ь—Л –љ–µ –њ–Њ–Љ–Њ–≥–∞–µ–Љ —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –Х—Б–ї–Є –љ–∞–є–і–µ—В–µ –њ–Њ—Е–Њ–ґ—Г—О –Ј–∞–і–∞—З—Г –љ–∞ —Б–∞–є—В–µ fipi.ru, –Њ—В–њ—А–∞–≤—М—В–µ –Ј–∞—П–≤–Ї—Г –љ–∞ –і–Њ–±–∞–≤–ї–µ–љ–Є–µ –Ј–∞–і–∞—З–Є, –Є –Љ—Л –µ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–±–∞–≤–Є–Љ.
(2020-04-13 11:07:18) –Ы—С—И–∞: –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –і–Є–∞–≥–Њ–љ–∞–ї—М AC –≤ 2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л AB –Є ∠ACD = 68¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
(2016-10-10 21:00:06) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р–љ–љ–∞, –Ь—Л –љ–µ –њ–Њ–Љ–Њ–≥–∞–µ–Љ —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –†–µ—И–Є—В–µ —Б–≤–Њ—О –Ј–∞–і–∞—З—Г –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ —Н—В–Њ–є.
(2016-10-10 19:48:19) –Р–љ–љ–∞: –≤ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ abcd –і–Є–∞–≥–Њ–љ–∞–ї—М –∞—Б –≤ 2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л –∞–≤ –Є —Г–≥–Њ–ї –∞—Б–і 127 –љ–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞
(2015-07-12 15:14:31) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ф–∞, –≤–µ—А–љ–Њ. –†–∞–љ—М—И–µ –њ—А–Њ—Б–Є–ї–Є –љ–∞–є—В–Є –Є–Љ–µ–љ–љ–Њ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї. –£—Б–ї–Њ–≤–Є–µ —Б–Ї–Њ—А—А–µ–Ї—В–Є—А–Њ–≤–∞–љ–Њ, —А–µ—И–µ–љ–Є–µ –і–Њ–њ–Њ–ї–љ–µ–љ–Њ. –°–њ–∞—Б–Є–±–Њ –Ј–∞ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—О.
(2015-07-02 13:20:03) : –≤ –Ј–∞–і–∞—З–µ –љ–∞ —Б–∞–є—В–µ "Fipi.ru" –љ–µ —Б–Ї–∞–Ј–∞–љ–Њ –љ–∞–є—В–Є –Ю–°–Ґ–†–Ђ–Щ —Г–≥–Њ–ї, —В–∞–Љ –њ—А–Њ—Б—В–Њ –љ–∞–є–і–Є—В–µ —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –і–Є–∞–≥–Њ–љ–∞–ї—П–Љ–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ => —Г–≥–Њ–ї –Љ–Њ–ґ–µ—В –±—Л—В—М –Є BOC
(2015-05-25 13:40:58) : –Э–Є—З–µ–≥–Њ –љ–µ –њ–Њ–љ—П—В–µ–Њ
(2015-03-25 15:03:13) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ф–Є–Љ–∞, –Є–Ј —Б—В—А–Њ–Ї–Є –≤—Л—И–µ. 180-104=76
(2015-03-24 12:19:17) –Ф–Є–Љ–∞: –Ю—В–Ї—Г–і–∞ 76 ?
(2015-03-24 12:19:16) –Ф–Є–Љ–∞: –Ю—В–Ї—Г–і–∞ 76 ?
(2014-05-27 20:39:20) —А–∞–Љ–∞–Ј–∞–љ: –Њ—В–≤–Є—В –і–∞–Є—В–Є