Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
Рассмотрим каждое утверждение.
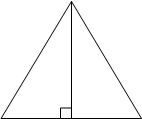
1) "У
равнобедренного треугольника есть ось симметрии", это утверждение верно, ось совпадает с
высотой, опущенной к основанию треугольника.
2) "Если в
параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат", это утверждение верно, т.к. оно совпадает со
свойством квадрата.
3) "Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности", это утверждение неверно, окружности не будут пересекаться, если, например, центры окружностей совпадают.
Поделитесь решением
Присоединяйтесь к нам...
Найдите угол ABC . Ответ дайте в градусах.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: