На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
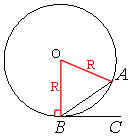Проведем радиусы к точкам A и B, как показано на рисунке.
∠AOB - центральный и опирается на дугу в 26°, следовательно:
∠AOB=26°
Треугольник AOB - равнобедренный, так как две его стороны - это радиусы окружности.
Тогда, по свойству равнобедренного треугольника, углы при основании равны, обозначим их α.
По
теореме о сумме углов треугольника:
∠AOB+∠OAB+∠OBA=180°
26°+α+α=180°
2α=180°-26°=154°
α=154°/2=77°
По
свойству касательной ∠OBC=90°.
∠ABC=∠OBC-∠OBA
∠ABC=90°-77°=13°
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
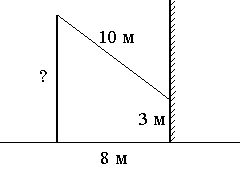От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
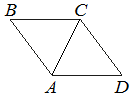В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: