
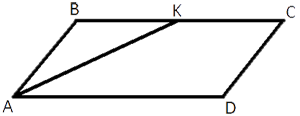 Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
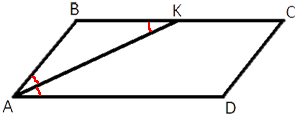 Стороны AD и BC параллельны по
определению параллелограмма.
Стороны AD и BC параллельны по
определению параллелограмма.
Тогда АК мы можем рассмотривать как секущую.
Тогда ∠DAK=∠BKA (так как они
накрест-лежащие).
ВК - вдвое меньше BC (т.к. К - середина).
AB тоже вдвое меньше BC (по условию).
Следовательно, BK=AB, т.е. треугольник ABK равнобедренный.
Тогда, по свойству равнобедренного треугольника, ∠BAK=∠BKA.
Получается, что ∠BAK=∠BKA=∠DAK.
Т.е. AK - биссектрисса.
Поделитесь решением
Присоединяйтесь к нам...
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
 Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1.
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его высотой.
2) Диагонали прямоугольника равны.
3) У любой трапеции основания параллельны.
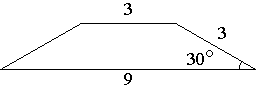 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.


Комментарии: