
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ226 –Η–Ζ 1087 |
 –‰–Ζ ―²–Ψ―΅–Κ–Η –ê –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –Κ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –ê –¥–Ψ ―²–Ψ―΅–Κ–Η –û, –Β―¹–Μ–Η ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η ―Ä–Α–≤–Β–Ϋ
60¬Α, –Α ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 6.
–‰–Ζ ―²–Ψ―΅–Κ–Η –ê –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –Κ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β –û. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –ê –¥–Ψ ―²–Ψ―΅–Κ–Η –û, –Β―¹–Μ–Η ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η ―Ä–Α–≤–Β–Ϋ
60¬Α, –Α ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–≤–Β–Ϋ 6.
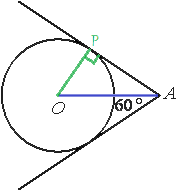 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –ê–û. –û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ –Ψ–¥–Ϋ―É –Η–Ζ ―²–Ψ―΅–Β–Κ –Κ–Α―¹–Α–Ϋ–Η―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Η –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι –Κ–Α–Κ –†. –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –û–†. –û–† ―è–≤–Μ―è–Β―²―¹―è ―Ä–Α–¥–Η―É―¹–Ψ–Φ –Η –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ψ–Φ –Κ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι –ê–† (–Ω–Ψ ―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι).
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –ê–û–†. –î–Α–Ϋ–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―è–≤–Μ―è–Β―²―¹―è –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Φ,―².–Κ. –û–† –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ –ê–†. –ê–û ―è–≤–Μ―è–Β―²―¹―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι ―É–≥–Μ–Α, –Ψ–±―Ä–Α–Ζ–Ψ–≤–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η (―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄―Ö –Ω―Ä―è–Φ―΄―Ö). –Γ–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ ―É–≥–Ψ–Μ –†–ê–û ―Ä–Α–≤–Β–Ϋ –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –¥–Α–Ϋ–Ϋ–Ψ–≥–Ψ ―É–≥–Μ–Α, ―².–Β. 30¬Α. –Γ–Η–Ϋ―É―¹ ―É–≥–Μ–Α PAO ―Ä–Α–≤–Β–Ϋ 1/2 (―²–Α–±–Μ–Η―΅–Ϋ–Ψ–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β) –Η ―Ä–Α–≤–Β–Ϋ –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η―é –û–† –Κ –ê–û (–Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é ―¹–Η–Ϋ―É―¹–Α). –Γ–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ, –û–† ―Ä–Α–≤–Ϋ―è–Β―²―¹―è –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –ê–û. AO=2*–û–†=2*6=12.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –ê–û. –û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ –Ψ–¥–Ϋ―É –Η–Ζ ―²–Ψ―΅–Β–Κ –Κ–Α―¹–Α–Ϋ–Η―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Η –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι –Κ–Α–Κ –†. –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ –û–†. –û–† ―è–≤–Μ―è–Β―²―¹―è ―Ä–Α–¥–Η―É―¹–Ψ–Φ –Η –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ψ–Φ –Κ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι –ê–† (–Ω–Ψ ―¹–≤–Ψ–Ι―¹―²–≤―É –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ–Ψ–Ι).
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –ê–û–†. –î–Α–Ϋ–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ―è–≤–Μ―è–Β―²―¹―è –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Φ,―².–Κ. –û–† –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ –ê–†. –ê–û ―è–≤–Μ―è–Β―²―¹―è –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Ψ–Ι ―É–≥–Μ–Α, –Ψ–±―Ä–Α–Ζ–Ψ–≤–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Φ–Η (―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄―Ö –Ω―Ä―è–Φ―΄―Ö). –Γ–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ ―É–≥–Ψ–Μ –†–ê–û ―Ä–Α–≤–Β–Ϋ –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –¥–Α–Ϋ–Ϋ–Ψ–≥–Ψ ―É–≥–Μ–Α, ―².–Β. 30¬Α. –Γ–Η–Ϋ―É―¹ ―É–≥–Μ–Α PAO ―Ä–Α–≤–Β–Ϋ 1/2 (―²–Α–±–Μ–Η―΅–Ϋ–Ψ–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β) –Η ―Ä–Α–≤–Β–Ϋ –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η―é –û–† –Κ –ê–û (–Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é ―¹–Η–Ϋ―É―¹–Α). –Γ–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ, –û–† ―Ä–Α–≤–Ϋ―è–Β―²―¹―è –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –ê–û. AO=2*–û–†=2*6=12.
–û―²–≤–Β―²: AO=12.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ö–Α―²–Β―²―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ―΄ 35 –Η 120. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ―É―é –Κ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Β.
–ö–Α―²–Β―²―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ―΄ 35 –Η 120. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É, –Ω―Ä–Ψ–≤–Β–¥―ë–Ϋ–Ϋ―É―é –Κ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Β.
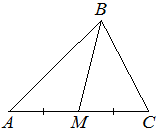 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ AC=14, BM βÄî –Φ–Β–¥–Η–Α–Ϋ–Α, BM=10. –ù–Α–Ι–¥–Η―²–Β AM.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ AC=14, BM βÄî –Φ–Β–¥–Η–Α–Ϋ–Α, BM=10. –ù–Α–Ι–¥–Η―²–Β AM.
 –ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 80 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 250 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η
(–≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö) –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 160 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η?
–ü―Ä–Ψ–Β–Κ―²–Ψ―Ä –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â–Α–Β―² ―ç–Κ―Ä–Α–Ϋ A –≤―΄―¹–Ψ―²–Ψ–Ι 80 ―¹–Φ, ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Ϋ―΄–Ι –Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η 250 ―¹–Φ –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α. –ù–Α –Κ–Α–Κ–Ψ–Φ –Ϋ–Α–Η–Φ–Β–Ϋ―¨―à–Β–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η
(–≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö) –Ψ―² –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ϋ―É–Ε–Ϋ–Ψ ―Ä–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Η―²―¨ ―ç–Κ―Ä–Α–Ϋ B –≤―΄―¹–Ψ―²–Ψ–Ι 160 ―¹–Φ, ―΅―²–Ψ–±―΄ –Ψ–Ϋ –±―΄–Μ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Ψ―¹–≤–Β―â―ë–Ϋ, –Β―¹–Μ–Η –Ϋ–Α―¹―²―Ä–Ψ–Ι–Κ–Η –Ω―Ä–Ψ–Β–Κ―²–Ψ―Ä–Α –Ψ―¹―²–Α―é―²―¹―è –Ϋ–Β–Η–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η?
 –û―²―Ä–Β–Ζ–Κ–Η AB –Η CD ―è–≤–Μ―è―é―²―¹―è ―Ö–Ψ―Ä–¥–Α–Φ–Η –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―Ü–Β–Ϋ―²―Ä–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –¥–Ψ ―Ö–Ψ―Ä–¥―΄ CD, –Β―¹–Μ–Η AB=20, CD=48, –Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―Ü–Β–Ϋ―²―Ä–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –¥–Ψ ―Ö–Ψ―Ä–¥―΄ AB ―Ä–Α–≤–Ϋ–Ψ 24.
–û―²―Ä–Β–Ζ–Κ–Η AB –Η CD ―è–≤–Μ―è―é―²―¹―è ―Ö–Ψ―Ä–¥–Α–Φ–Η –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―Ü–Β–Ϋ―²―Ä–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –¥–Ψ ―Ö–Ψ―Ä–¥―΄ CD, –Β―¹–Μ–Η AB=20, CD=48, –Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―Ü–Β–Ϋ―²―Ä–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –¥–Ψ ―Ö–Ψ―Ä–¥―΄ AB ―Ä–Α–≤–Ϋ–Ψ 24.
 –Δ–Ψ―΅–Κ–Η M –Η N ―è–≤–Μ―è―é―²―¹―è ―¹–Β―Ä–Β–¥–Η–Ϋ–Α–Φ–Η ―¹―²–Ψ―Ä–Ψ–Ϋ AB –Η BC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –û―²―Ä–Β–Ζ–Κ–Η AN
–Η CM –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β O, AN=27, CM=9. –ù–Α–Ι–¥–Η―²–Β AO.
–Δ–Ψ―΅–Κ–Η M –Η N ―è–≤–Μ―è―é―²―¹―è ―¹–Β―Ä–Β–¥–Η–Ϋ–Α–Φ–Η ―¹―²–Ψ―Ä–Ψ–Ϋ AB –Η BC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –û―²―Ä–Β–Ζ–Κ–Η AN
–Η CM –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β O, AN=27, CM=9. –ù–Α–Ι–¥–Η―²–Β AO.
| α | sinα | cosα | tgα | ctgα |
| 0¬Α | 0 | 1 | 0 | --- |
| 30¬Α | 1/2 | √ |
√ |
√ |
| 45¬Α | √ |
√ |
1 | 1 |
| 60¬Α | √ |
1/2 | √ |
√ |
| 90¬Α | 1 | 0 | --- | 0 |
| 120¬Α | √ |
-1/2 | -√ |
0 |
| 135¬Α | √ |
-√ |
-1 | -1 |
| 150¬Α | 1/2 | -√ |
-√ |
-√ |
| 180¬Α | 0 | -1 | 0 | --- |
| 210¬Α | -1/2 | -√ |
√ |
√ |
| 225¬Α | -√ |
-√ |
1 | 1 |
| 240¬Α | -√ |
-1/2 | √ |
√ |
| 270¬Α | -1 | 0 | --- | 0 |
| 300¬Α | -√ |
1/2 | -√ |
-√ |
| 315¬Α | -√ |
√ |
-1 | -1 |
| 330¬Α | -1/2 | √ |
-√ |
-√ |
| 360¬Α | 1 | 0 | 0 | --- |
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: