
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ561 –Η–Ζ 1087 |
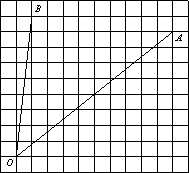 –ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α
AOB.
–ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α
AOB.
–£–Α―Ä–Η–Α–Ϋ―² ⳕ1 (–ü―Ä–Η―¹–Μ–Α–Μ –Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²–Β–Μ―¨ –ï–≤–≥–Β–Ϋ–Η–Ι)
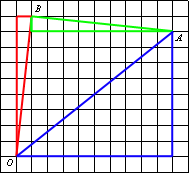 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ AB.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Ψ–Κ AB.
–ù–Α–Ι–¥–Β–Φ –Κ–Α–Ε–¥―É―é ―¹―²–Ψ―Ä–Ψ–Ϋ―É ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABO –Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
AO2=102+82
AO2=100+64=164
AO=√
AB2=92+12
AB2=81+1=82
AB=√
BO2=92+12
BO2=81+1=82
BO=√
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–≤:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
82=164+82-2√
-164=-2√
82=√
82=2√
41=√
cos∠AOB=41/√
–ü–Ψ –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Ψ–Ι ―²―Ä–Η–≥–Ψ–Ϋ–Ψ–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Ψ–Ι ―³–Ψ―Ä–Φ―É–Μ–Β:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(1/√
sin2∠AOB+1/2=1
sin2∠AOB=1/2
sin∠AOB=1/√
tg∠AOB=sin∠AOB/cos∠AOB=(1/√
–û―²–≤–Β―²: tg∠AOB=1
 –î–Ψ―¹―²―Ä–Ψ–Η–Φ ―΅–Β―Ä―²–Β–Ε –¥–Ψ –¥–≤―É―Ö
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤. –ù–Α–Ι–¥–Β–Φ
―²–Α–Ϋ–≥–Β–Ϋ―¹―΄ –¥–Μ―è –Ψ–±–Ψ–Η―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ –¥–Μ―è –Η―Ö ―É–≥–Μ–Ψ–≤ –û.
–î–Ψ―¹―²―Ä–Ψ–Η–Φ ―΅–Β―Ä―²–Β–Ε –¥–Ψ –¥–≤―É―Ö
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤. –ù–Α–Ι–¥–Β–Φ
―²–Α–Ϋ–≥–Β–Ϋ―¹―΄ –¥–Μ―è –Ψ–±–Ψ–Η―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤ –¥–Μ―è –Η―Ö ―É–≥–Μ–Ψ–≤ –û.–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
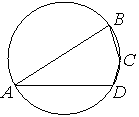 –Θ–≥–Ψ–Μ A ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABCD, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–≥–Ψ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, ―Ä–Α–≤–Β–Ϋ 33¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ C ―ç―²–Ψ–≥–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–Θ–≥–Ψ–Μ A ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABCD, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–≥–Ψ –≤ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨, ―Ä–Α–≤–Β–Ϋ 33¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ C ―ç―²–Ψ–≥–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
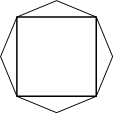 –î–Α–Ϋ –Ω―Ä–Α–≤–Η–Μ―¨–Ϋ―΄–Ι –≤–Ψ―¹―¨–Φ–Η―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –Β―¹–Μ–Η –Β–≥–Ψ –≤–Β―Ä―à–Η–Ϋ―΄ –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―¹–Ψ–Β–¥–Η–Ϋ–Η―²―¨ –Ψ―²―Ä–Β–Ζ–Κ–Α–Φ–Η ―΅–Β―Ä–Β–Ζ –Ψ–¥–Ϋ―É, ―²–Ψ –Ω–Ψ–Μ―É―΅–Η―²―¹―è –Κ–≤–Α–¥―Ä–Α―².
–î–Α–Ϋ –Ω―Ä–Α–≤–Η–Μ―¨–Ϋ―΄–Ι –≤–Ψ―¹―¨–Φ–Η―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –Β―¹–Μ–Η –Β–≥–Ψ –≤–Β―Ä―à–Η–Ϋ―΄ –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―¹–Ψ–Β–¥–Η–Ϋ–Η―²―¨ –Ψ―²―Ä–Β–Ζ–Κ–Α–Φ–Η ―΅–Β―Ä–Β–Ζ –Ψ–¥–Ϋ―É, ―²–Ψ –Ω–Ψ–Μ―É―΅–Η―²―¹―è –Κ–≤–Α–¥―Ä–Α―².
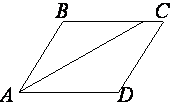 –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É –Ψ―¹―²―Ä–Ψ–≥–Ψ ―É–≥–Μ–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD, –Β―¹–Μ–Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α A –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι BC ―É–≥–Ψ–Μ, ―Ä–Α–≤–Ϋ―΄–Ι 14¬Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É –Ψ―¹―²―Ä–Ψ–≥–Ψ ―É–≥–Μ–Α –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD, –Β―¹–Μ–Η –±–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α ―É–≥–Μ–Α A –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι BC ―É–≥–Ψ–Μ, ―Ä–Α–≤–Ϋ―΄–Ι 14¬Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –ü―Ä―è–Φ–Α―è AD, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α―è –Φ–Β–¥–Η–Α–Ϋ–Β –£–€ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ, –¥–Β–Μ–Η―² –Β―ë –Ω–Ψ–Ω–Ψ–Μ–Α–Φ. –ù–Α–Ι–¥–Η―²–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―É –ê–Γ, –Β―¹–Μ–Η ―¹―²–Ψ―Ä–Ψ–Ϋ–Α –ê–£ ―Ä–Α–≤–Ϋ–Α 4.
–ü―Ä―è–Φ–Α―è AD, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α―è –Φ–Β–¥–Η–Α–Ϋ–Β –£–€ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ, –¥–Β–Μ–Η―² –Β―ë –Ω–Ψ–Ω–Ψ–Μ–Α–Φ. –ù–Α–Ι–¥–Η―²–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―É –ê–Γ, –Β―¹–Μ–Η ―¹―²–Ψ―Ä–Ψ–Ϋ–Α –ê–£ ―Ä–Α–≤–Ϋ–Α 4.
 –ö–Α―²–Β―²―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ―΄ √
–ö–Α―²–Β―²―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ―΄ √





–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: